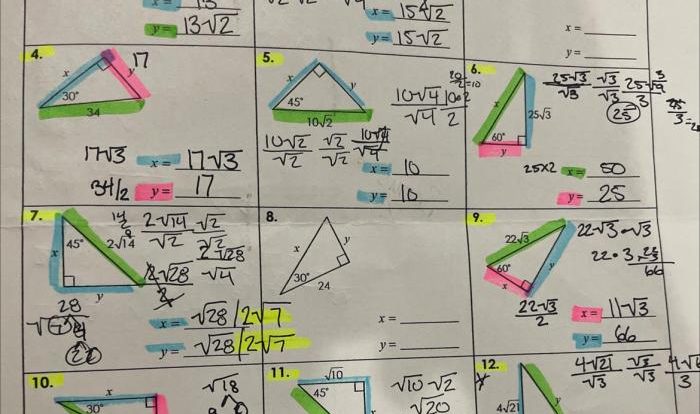
The special segments of a triangle worksheet embarks on an illuminating journey into the realm of geometry, unraveling the intricacies of these fundamental elements that define the structure and properties of triangles.

These special segments, namely medians, altitudes, perpendicular bisectors, and angle bisectors, hold profound significance in shaping the characteristics of triangles. Through their unique properties and relationships, they serve as invaluable tools for solving a myriad of geometric problems.

Special Segments of a Triangle

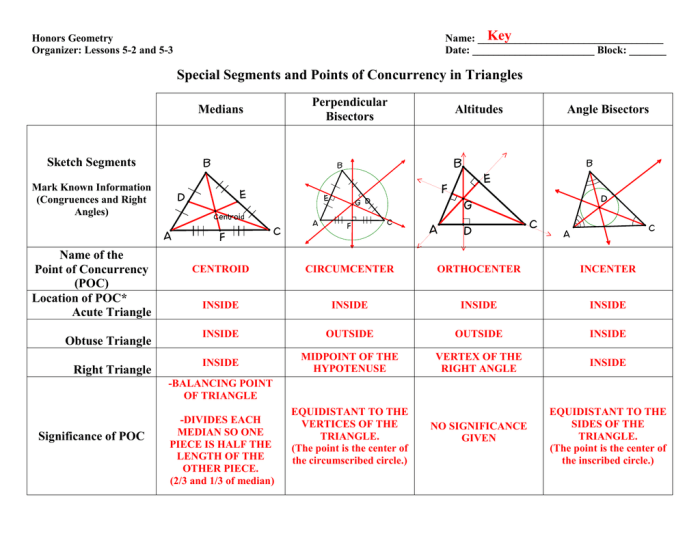
A triangle has several special segments that can be used to find important information about the triangle. These segments include the median, altitude, perpendicular bisector, and angle bisector.

Median

A median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side. There are three medians in a triangle, each connecting one vertex to the midpoint of the opposite side.

• Properties:
  • The median divides the triangle into two equal areas.
  • The median is concurrent at a point called the centroid.
  • The centroid divides the median in a 2:1 ratio.

Altitude, Special segments of a triangle worksheet

An altitude is a line segment that is perpendicular to a side of a triangle and passes through the opposite vertex. There are three altitudes in a triangle, each perpendicular to one side.

• Properties:
  • The altitude divides the triangle into two right triangles.
  • The altitude is concurrent at a point called the orthocenter.
  • The orthocenter may be inside or outside the triangle.

Perpendicular Bisector

A perpendicular bisector is a line segment that is perpendicular to a side of a triangle and passes through the midpoint of that side. There are three perpendicular bisectors in a triangle, each perpendicular to one side.

• Properties:
  • The perpendicular bisector divides the side into two equal segments.
  • The perpendicular bisector is concurrent at a point called the circumcenter.
  • The circumcenter is the center of the circle that circumscribes the triangle.

Angle Bisector

An angle bisector is a line segment that divides an angle of a triangle into two equal angles. There are three angle bisectors in a triangle, each dividing one angle into two equal angles.

• Properties:
  • The angle bisector divides the angle into two equal angles.
  • The angle bisector is concurrent at a point called the incenter.
  • The incenter is the center of the circle that is inscribed in the triangle.

Essential FAQs: Special Segments Of A Triangle Worksheet

What are the four types of special segments in a triangle?

The four types of special segments in a triangle are medians, altitudes, perpendicular bisectors, and angle bisectors.

What is the significance of special segments in triangle geometry?

Special segments play a crucial role in triangle geometry as they possess unique properties that allow for the determination of side lengths, angles, and other geometric characteristics.