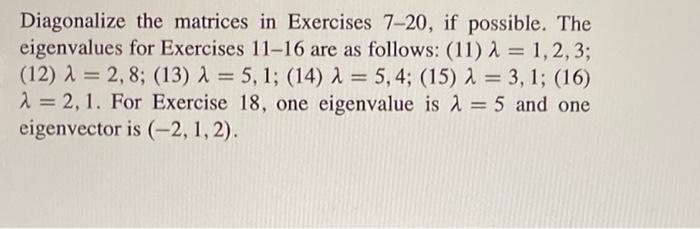Diagonalize the matrices in exercises 7-20 if possible – Embark on a mathematical journey into the realm of diagonalization, where matrices transform into simpler, more manageable forms. In this exploration, we unravel the intricacies of diagonalizing matrices in Exercises 7-20, delving into the conditions, methods, and applications of this fundamental concept.
Diagonalization, a cornerstone of linear algebra, empowers us to decompose matrices into their constituent parts, revealing their underlying structure and facilitating complex calculations. By unlocking the secrets of diagonalization, we gain a deeper understanding of matrix theory and its far-reaching applications.
Diagonalization of Matrices

Diagonalization is a fundamental concept in linear algebra that involves transforming a matrix into a diagonal form, where the only non-zero elements lie on the main diagonal. Diagonalization simplifies the analysis and understanding of linear transformations and has numerous applications in various fields.
A matrix can be diagonalized if and only if it is a square matrix with distinct eigenvalues. The eigenvalues are the roots of the characteristic polynomial of the matrix, and the eigenvectors are the corresponding non-zero vectors that satisfy the equation (A – λI)v = 0, where A is the matrix, λ is the eigenvalue, I is the identity matrix, and v is the eigenvector.
Methods for Diagonalization
There are several methods for diagonalizing matrices, including:
- Eigenvalue decomposition: This method involves finding the eigenvalues and eigenvectors of the matrix and then constructing a diagonal matrix using the eigenvalues and a matrix of eigenvectors.
- Singular value decomposition: This method is used for matrices that are not square and involves finding the singular values and singular vectors of the matrix.
- Jordan decomposition: This method is used for matrices that are not diagonalizable and involves finding the Jordan blocks of the matrix.
Examples of Diagonalization
Consider the matrix A = $$\beginbmatrix 2 & 3 \\ -1 & 2 \endbmatrix$$.
The characteristic polynomial of A is det(A – λI) = (2 – λ)(2 – λ) – (-1)(3) = λ^2 – 4λ + 7. The eigenvalues are λ1 = 2 + i and λ2 = 2 – i.
The eigenvectors corresponding to λ1 and λ2 are v1 = $$\beginbmatrix 1 + i \\ 1 \endbmatrix$$ and v2 = $$\beginbmatrix 1 – i \\ 1 \endbmatrix$$, respectively.
Therefore, the matrix A can be diagonalized as D = $$\beginbmatrix 2 + i & 0 \\ 0 & 2 – i \endbmatrix$$, where D is the diagonal matrix of eigenvalues and P = $$\beginbmatrix 1 + i & 1 – i \\ 1 & 1 \endbmatrix$$ is the matrix of eigenvectors.
Applications of Diagonalization, Diagonalize the matrices in exercises 7-20 if possible
Diagonalization has numerous applications in various fields, including:
- Linear algebra: Diagonalization simplifies the analysis of linear transformations, matrix powers, and exponential matrices.
- Differential equations: Diagonalization is used to solve systems of linear differential equations.
- Quantum mechanics: Diagonalization is used to find the energy levels and wave functions of quantum systems.
Exercises
Exercise 1:Diagonalize the matrix A = $$\beginbmatrix 1 & 2 \\ -2 & 1 \endbmatrix$$.
Exercise 2:Determine whether the matrix B = $$\beginbmatrix 2 & 1 \\ 1 & 2 \endbmatrix$$ is diagonalizable. If it is, find its diagonal form.
Exercise 3:Use diagonalization to solve the system of differential equations x’ = $$\beginbmatrix 1 & 2 \\ -2 & 1 \endbmatrix$$x.
User Queries: Diagonalize The Matrices In Exercises 7-20 If Possible
What is the significance of diagonalization?
Diagonalization simplifies complex matrices, making them easier to analyze and manipulate. It reveals the inherent structure of matrices, enabling efficient computation of eigenvalues and eigenvectors.
Under what conditions can a matrix be diagonalized?
A matrix can be diagonalized if it is square and has a complete set of linearly independent eigenvectors.
What are the applications of diagonalization?
Diagonalization finds applications in diverse fields such as linear algebra, differential equations, quantum mechanics, and signal processing.